19. 2 кучи.
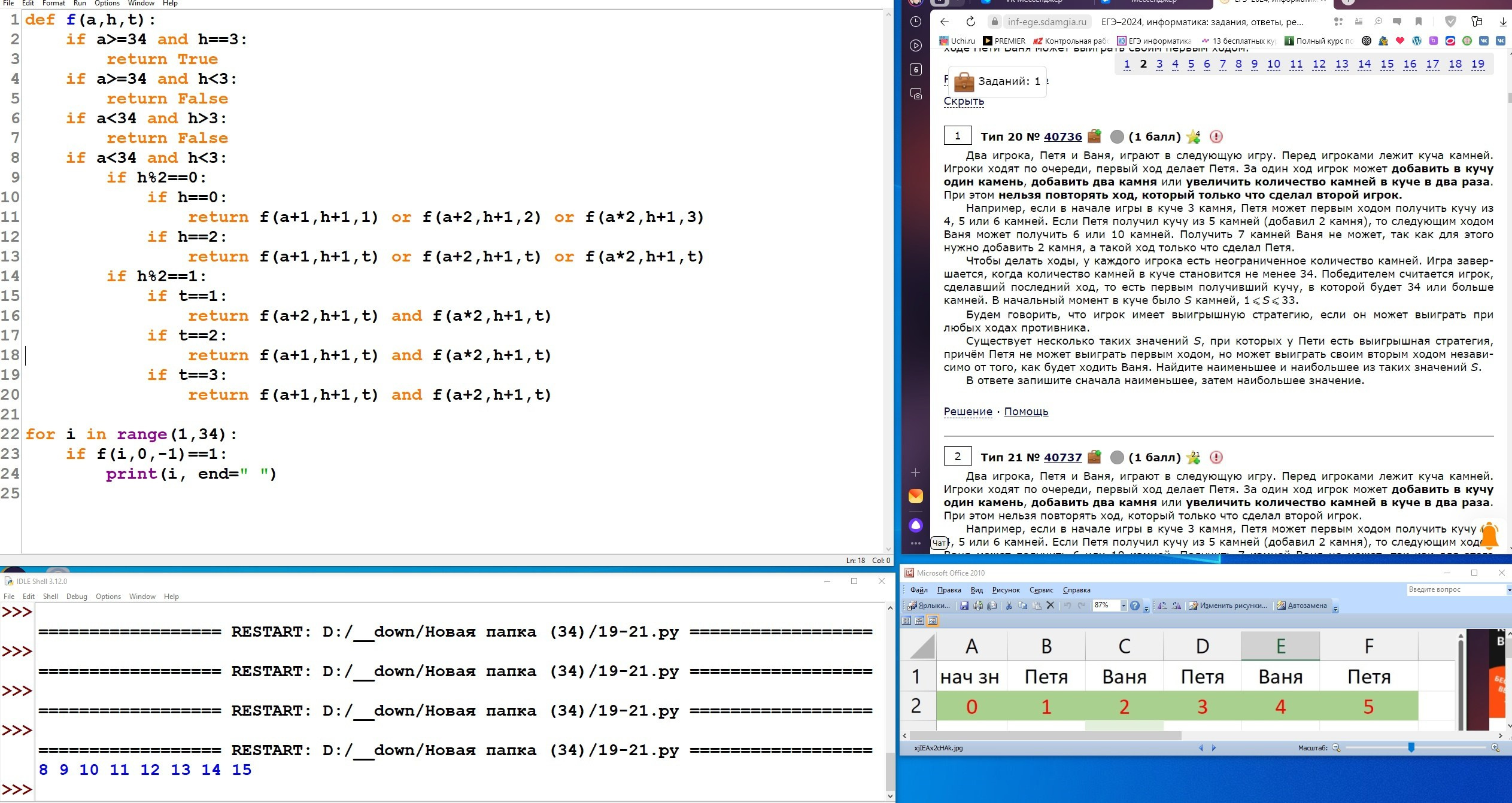
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 3: #Условия завершения игры
return p == 3
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or\
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 +
1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)
break
____________________________________
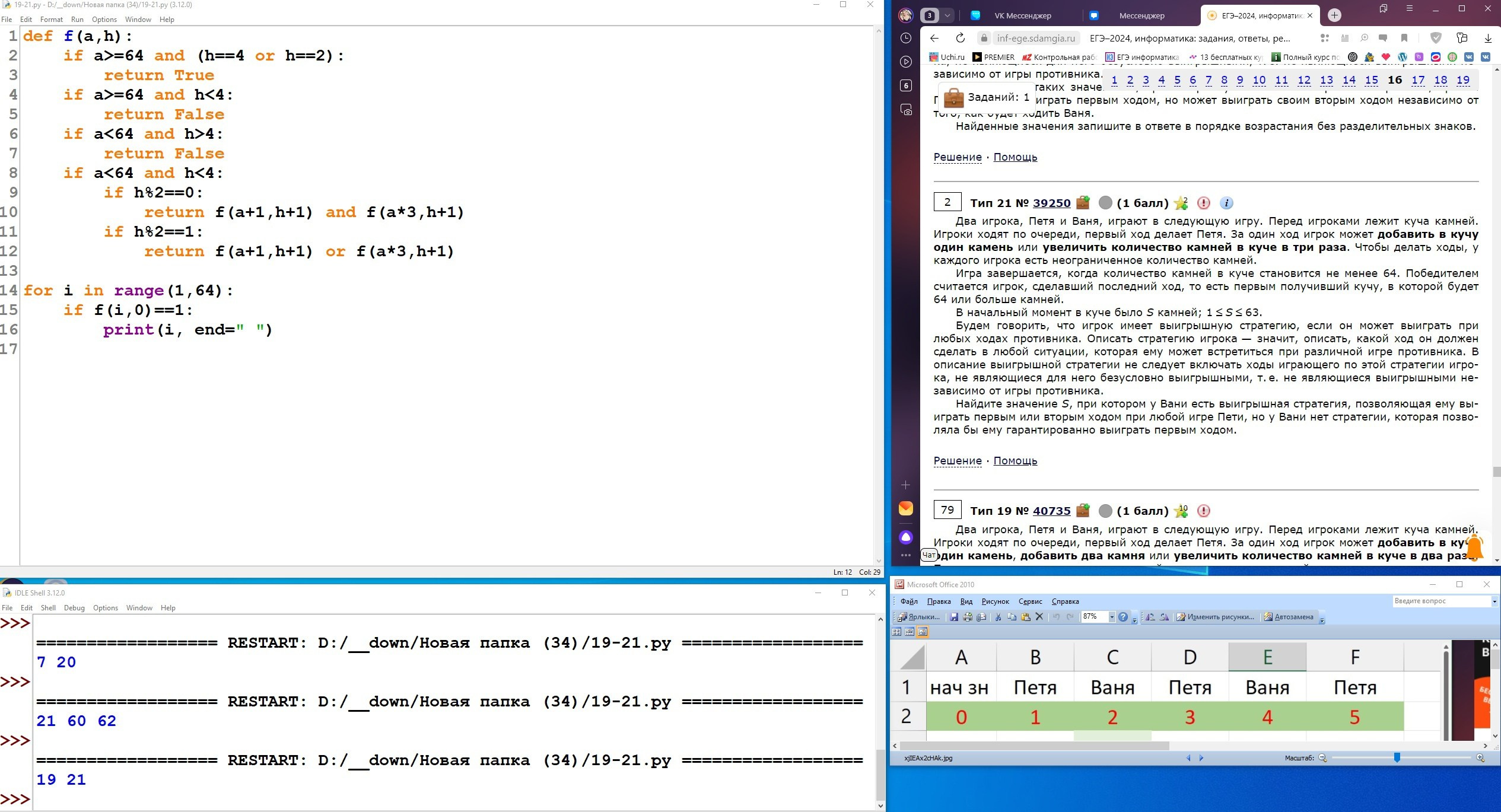
def e(x1,x2,s):
if x1+x2>=77 and s==3:
return True
else:
if x1+x2<77 and s==3:
return False
return e(x1+1,x2,s+1) or e(x1,x2+1,s+1) or e(x1*2,x2,s+1) or e(x1,x2*2,s+1)
for i in range
(1,150+1):
if e(7,i, 1):
print(i)
break
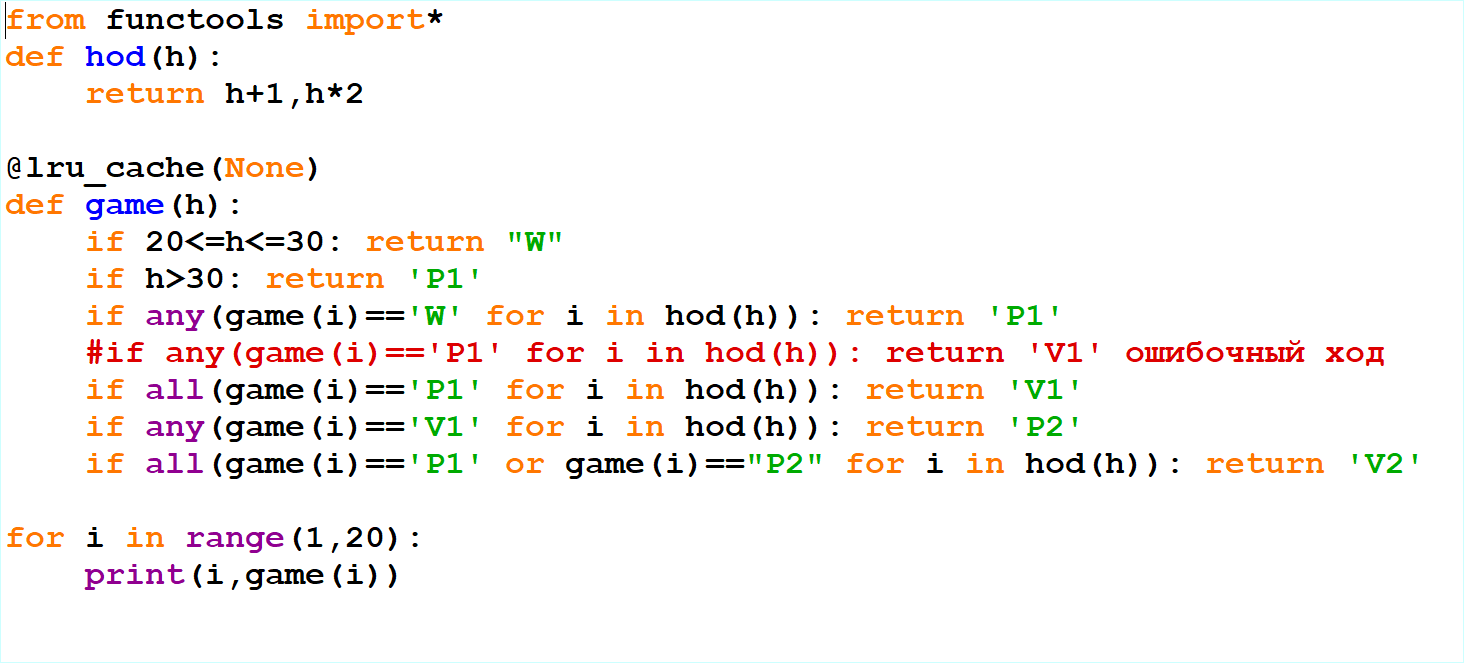
20. 1 куча. Сложное. С флагом.
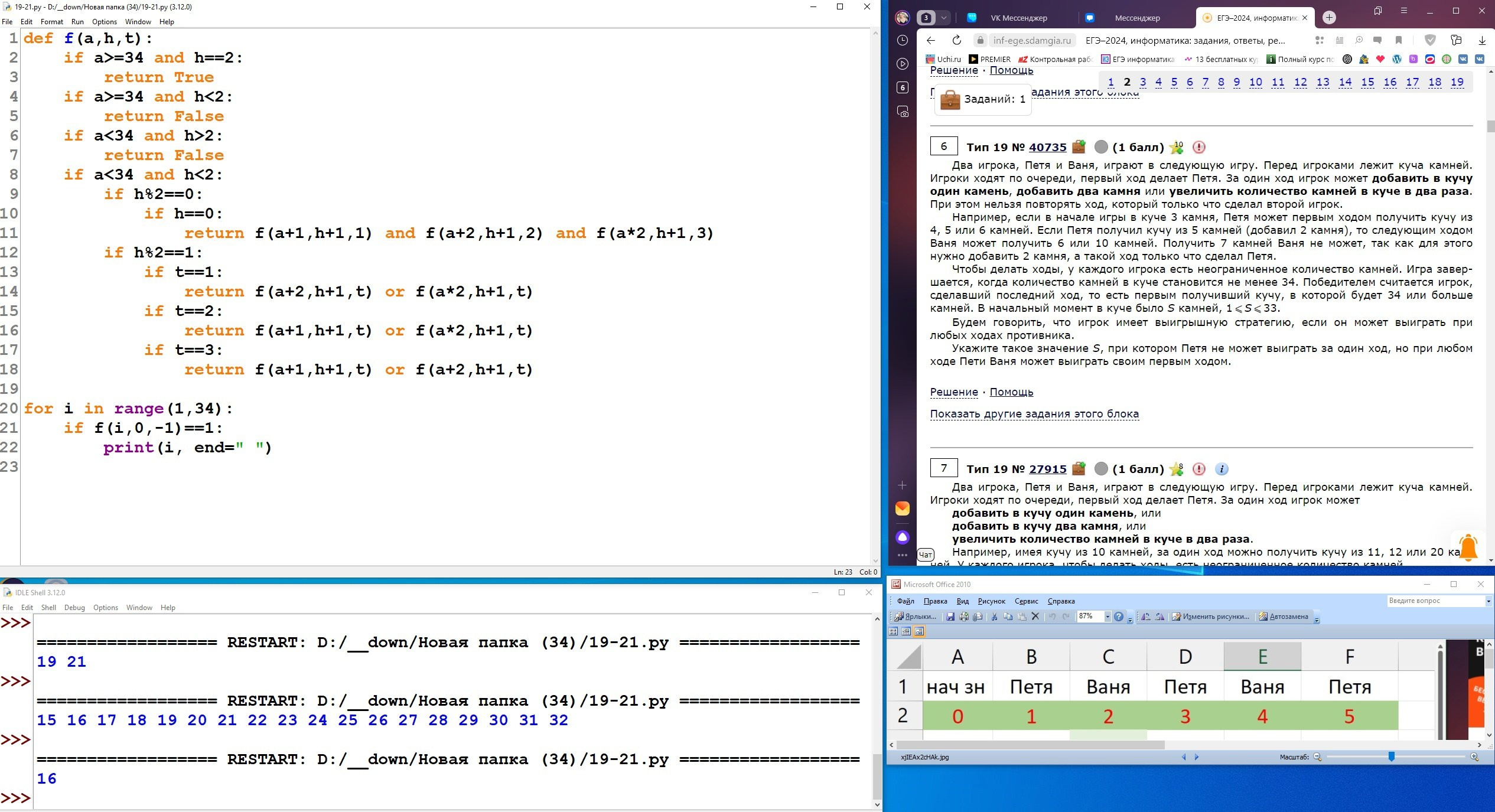
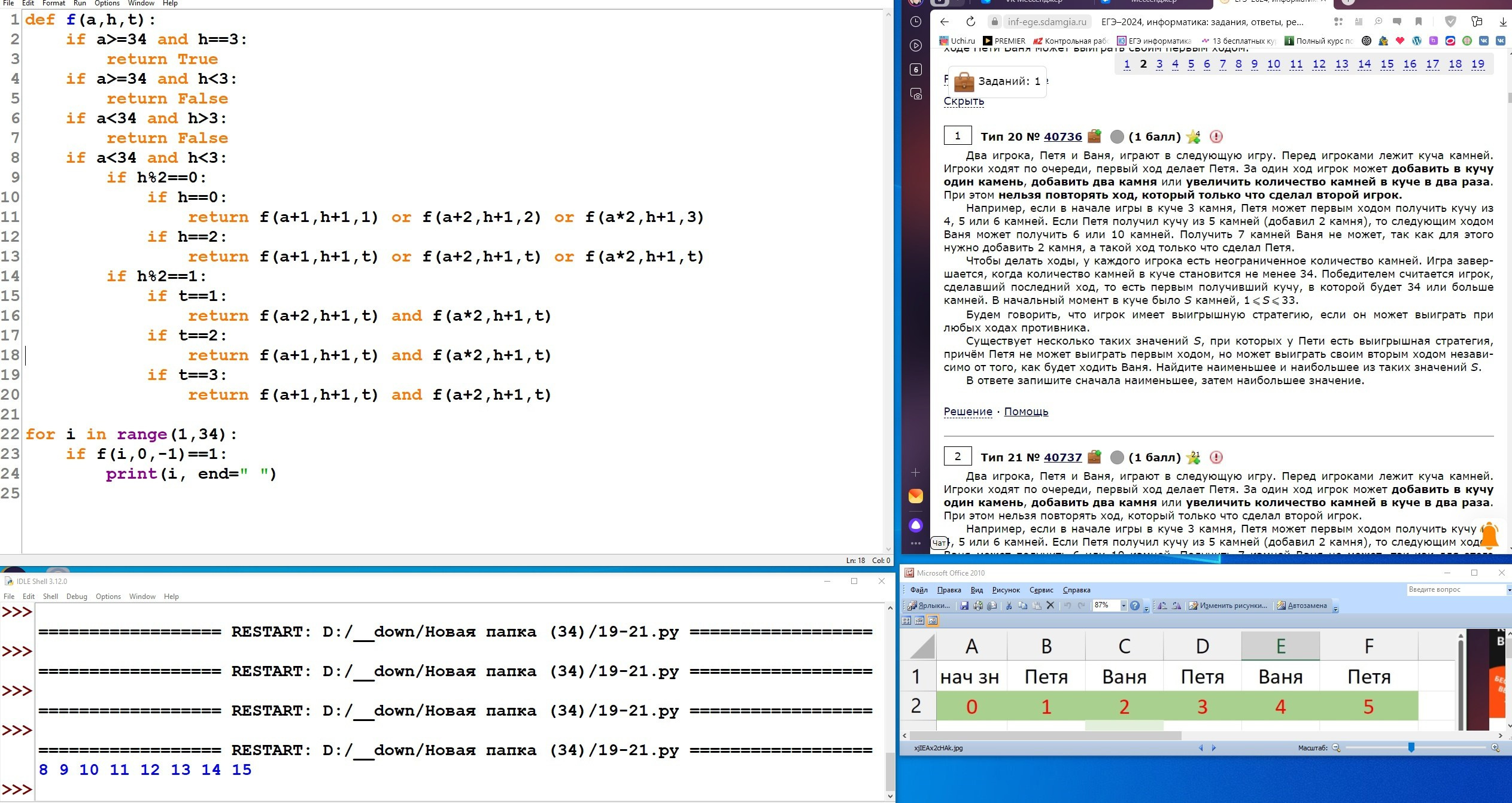
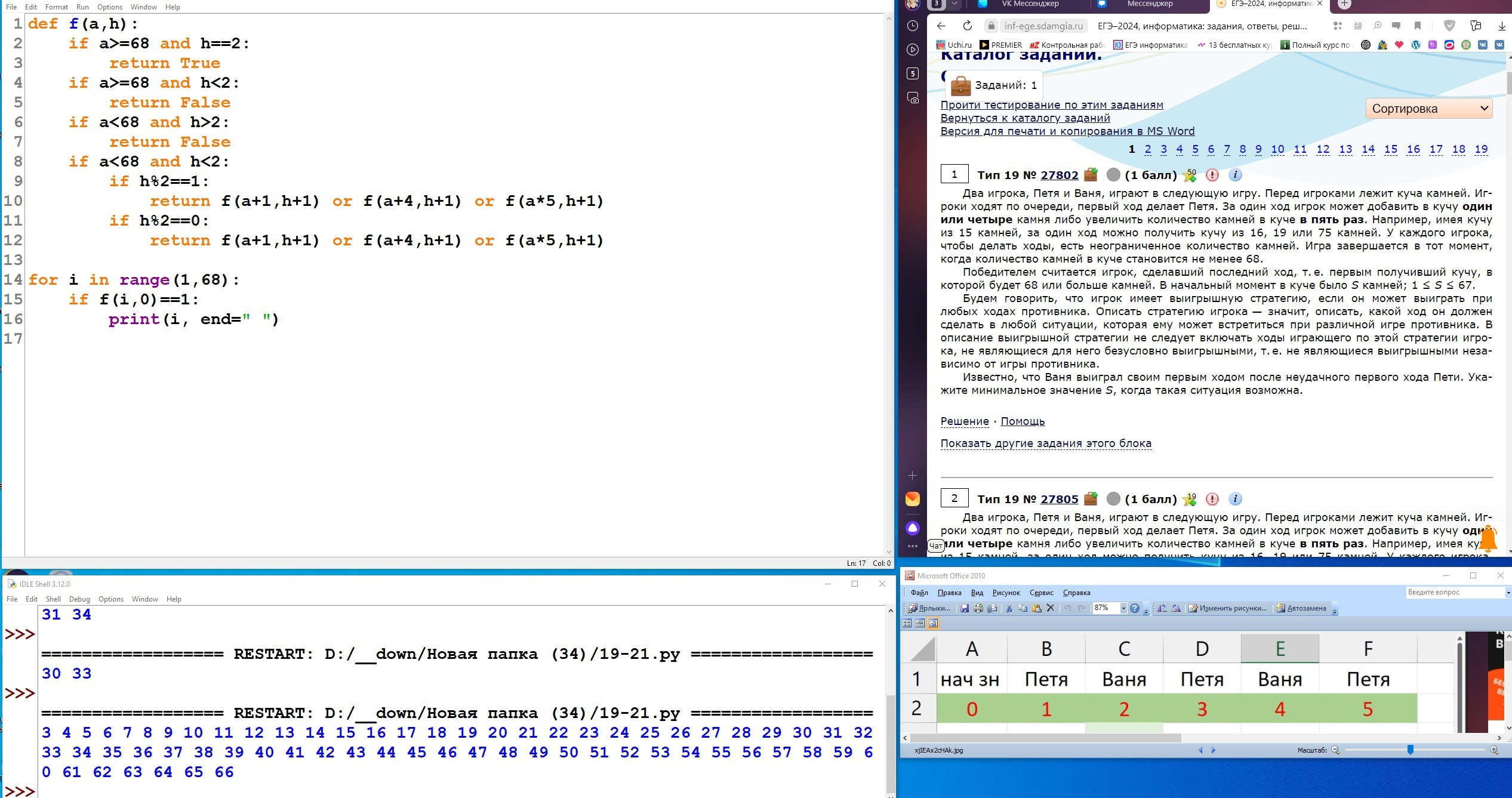
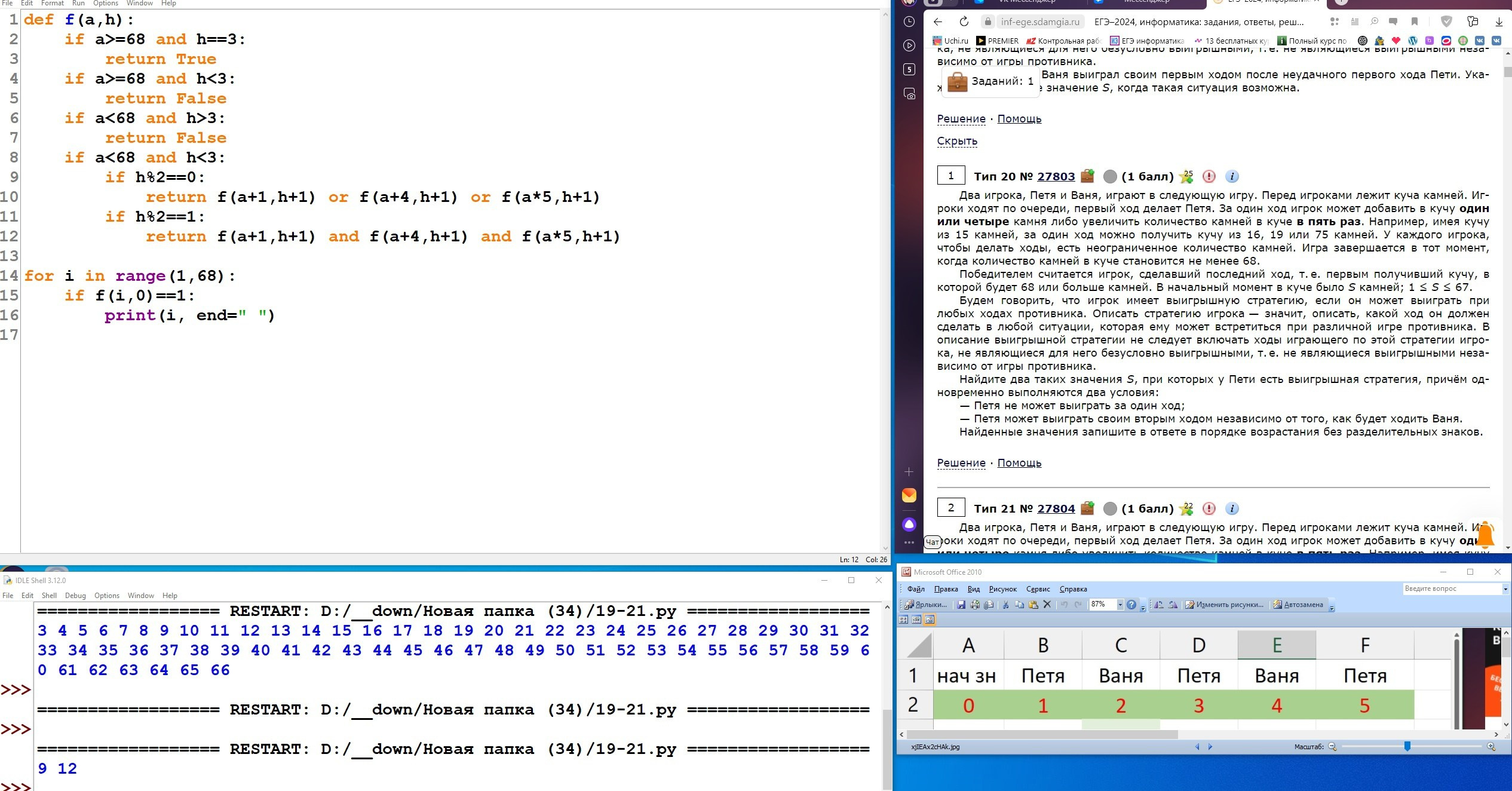
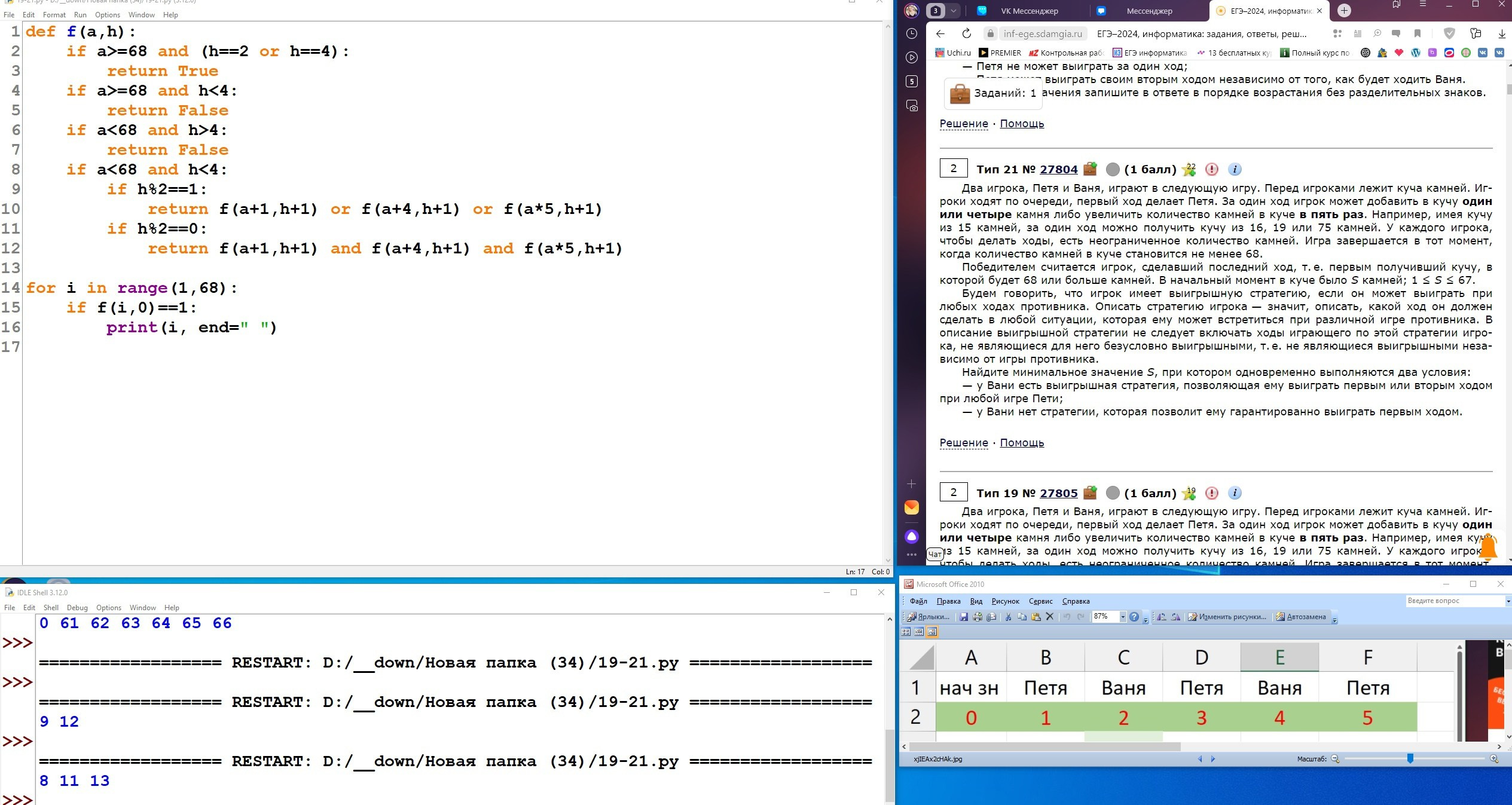
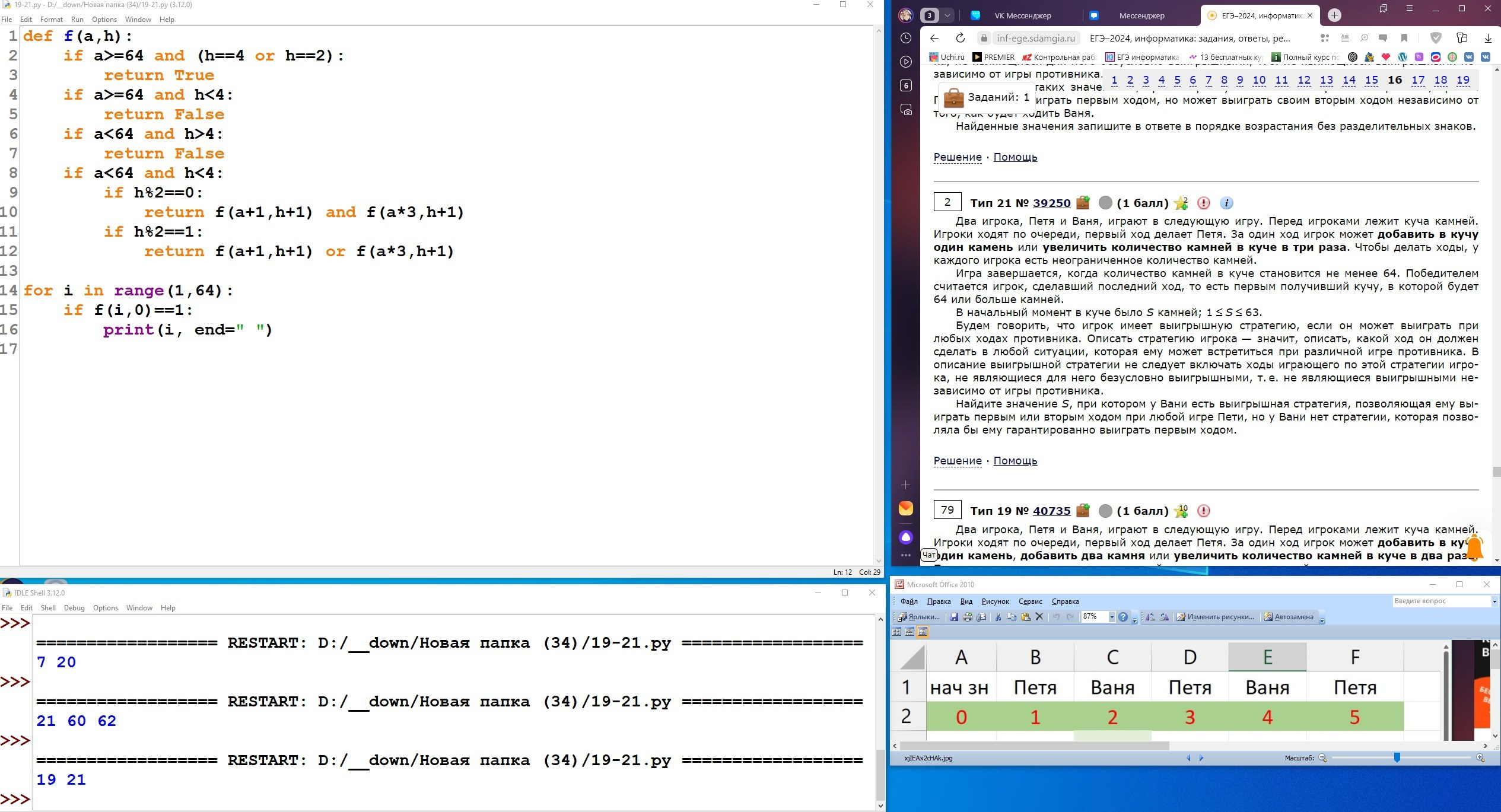
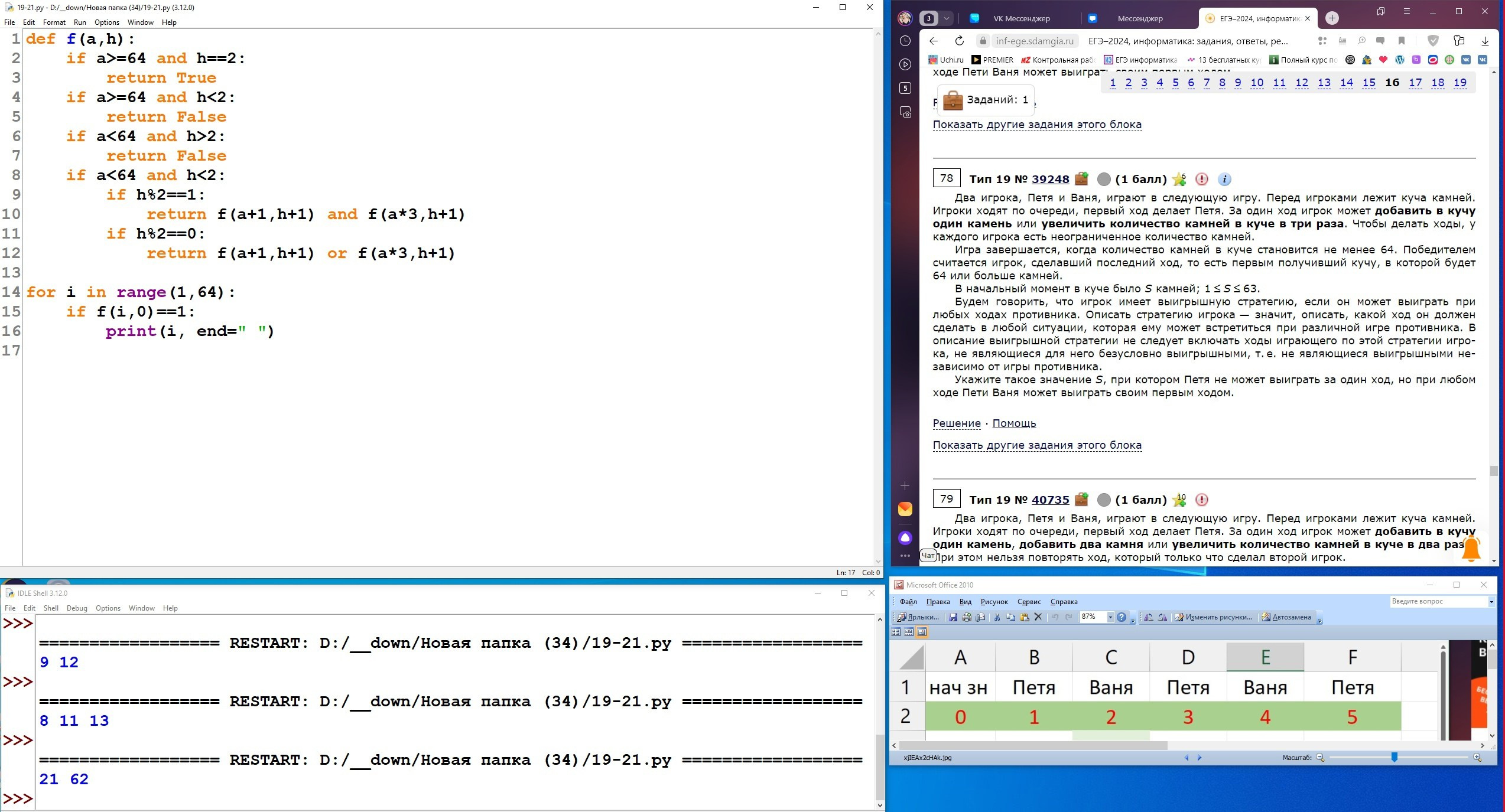
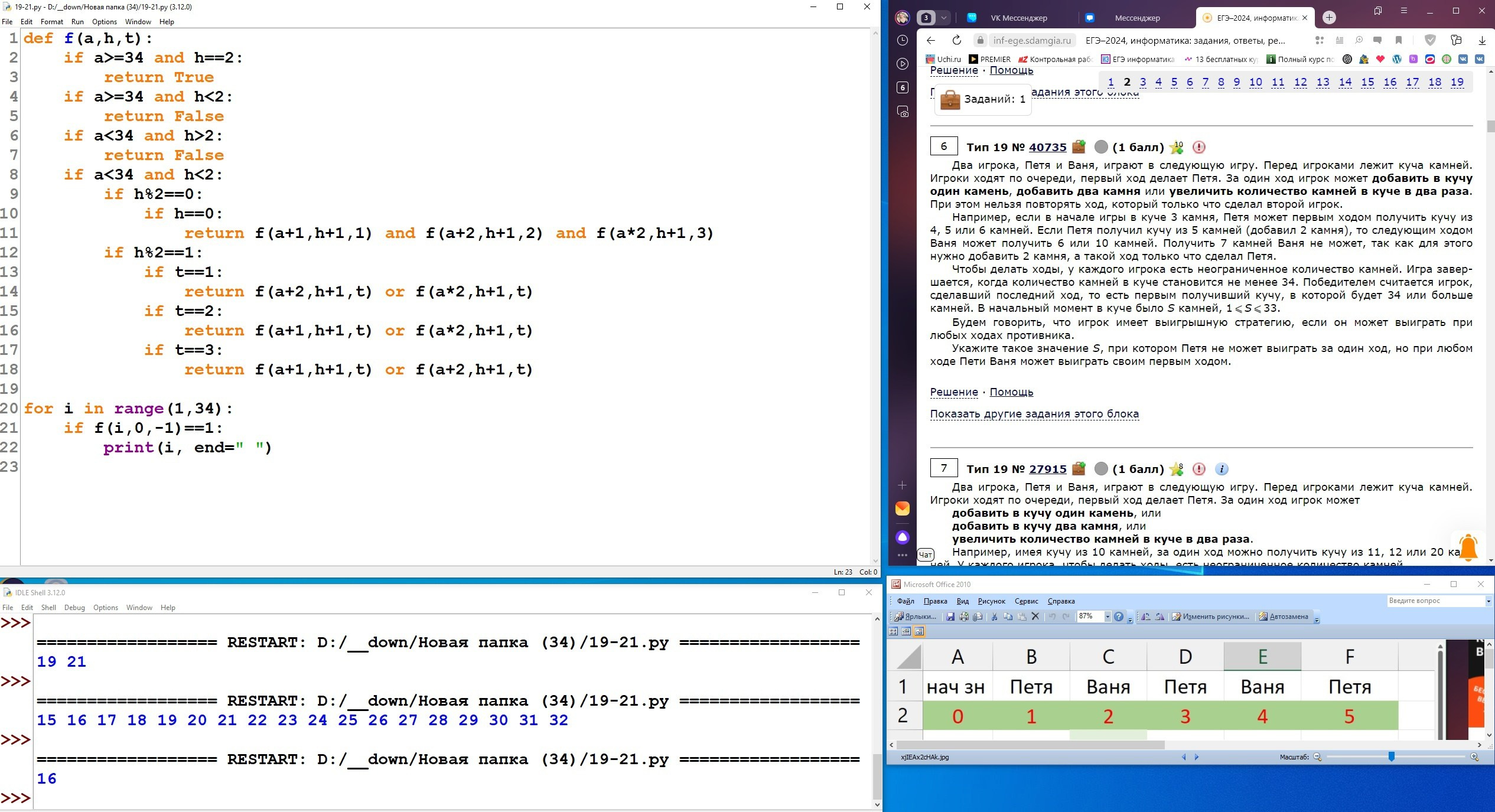
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить два камня или увеличить количество камней в куче в два раза. При этом нельзя повторять ход, который этот же игрок делал на предыдущем ходу. Повторять чужие ходы и свои более старые ходы разрешается.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ⩽ S ⩽ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите два значения S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть вторым ходом при любой игре Пети, но у Вани нет стратегии, которая позволяла бы ему гарантированно выиграть первым ходом.
В ответе запишите найденные значения в порядке возрастания: сначала меньшее, затем большее.
def f(x, h, p, v):
if (h == 5 or h == 3) and x >= 29:
return 1
elif h == 5 and x < 29:
return 0
elif x >= 29 and h < 5:
return 0
else:
if h % 2 == 0:
if h == 2:
return f(x + 1, h + 1, p, 1) or f(x + 2, h + 1, p, 2) or f(x * 2, h + 1, p, 3) # стратегия победителя
elif h == 4:
if v == 1:
return f(x + 2, h + 1, p, v) or f(x * 2, h + 1, p, v)
elif v == 2:
return f(x + 1, h + 1, p, v) or f(x * 2, h + 1, p, v)
elif v == 3:
return f(x + 1, h + 1, p, v) or f(x + 2, h + 1, p, v)
else: # Петин ход
if h == 1:
return f(x + 1, h + 1, 1, v) and f(x + 2, h + 1, 2, v) and f(x * 2, h + 1, 3, v) # стратегия победителя
elif h == 3:
if p == 1:
return f(x + 2, h + 1, p, v) and f(x * 2, h + 1, p, v)
elif p == 2:
return f(x + 1, h + 1, p, v) and f(x * 2, h + 1, p, v)
elif p == 3:
return f(x + 1, h + 1, p, v) and f(x + 2, h + 1, p, v)
for x in range(1, 29):
if f(x, 1, 0, 0) == 1:
print(«Задача 20:», x)
# Исключаем победу Вани только первым ходом
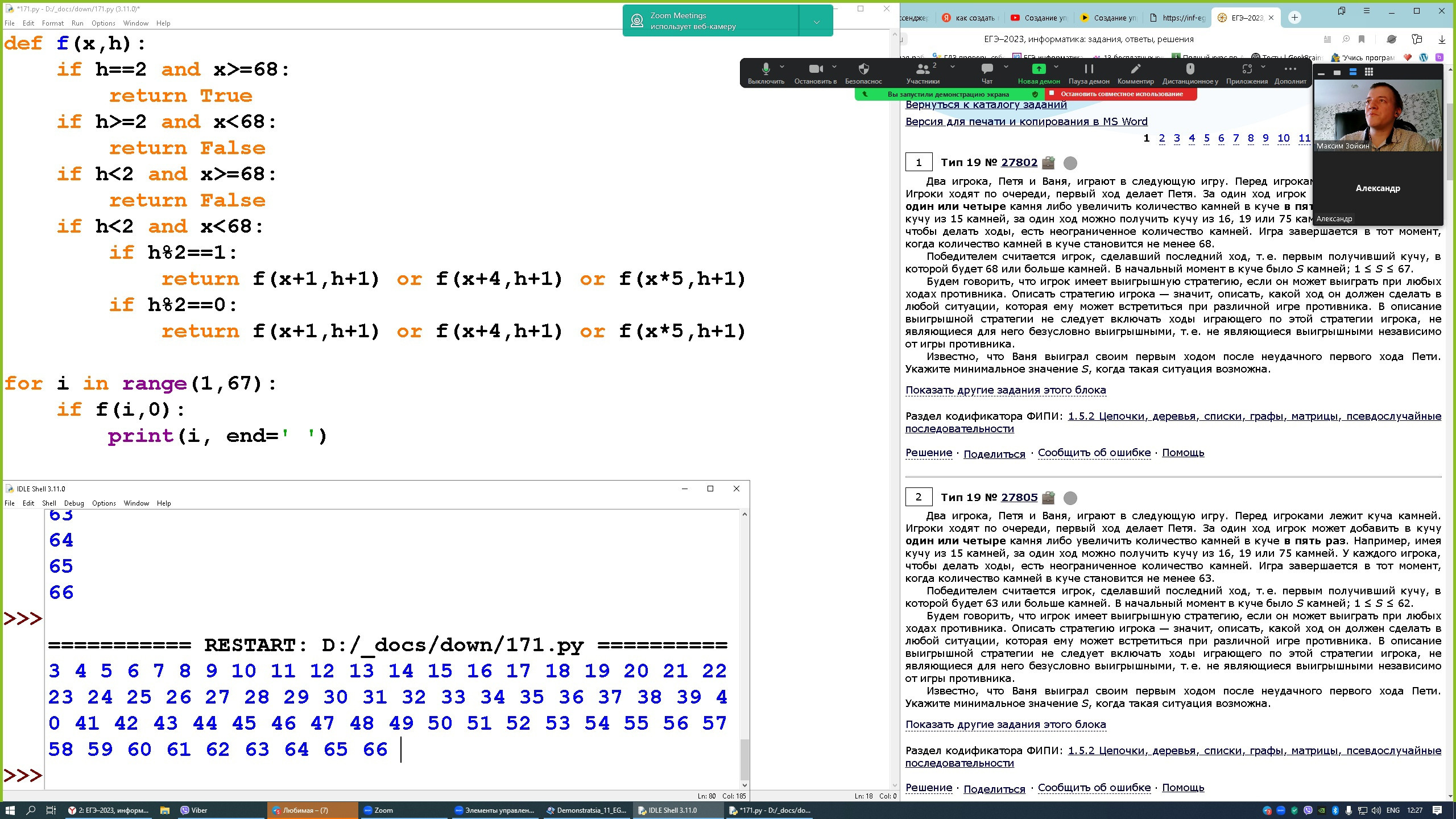
def f(x, h):
if h == 3 and x >= 29:
return 1
elif h == 3 and x < 29:
return 0
elif x >= 29 and h < 3:
return 0
else:
if h % 2 == 0:
return f(x + 1, h + 1) or f(x + 2, h + 1) or f(x * 2, h + 1) # стратегия победителя
else:
return f(x + 1, h + 1) and f(x + 2, h + 1) and f(x * 2, h + 1) # стратегия проигравшего (любой ход)
20. 2 кучи.
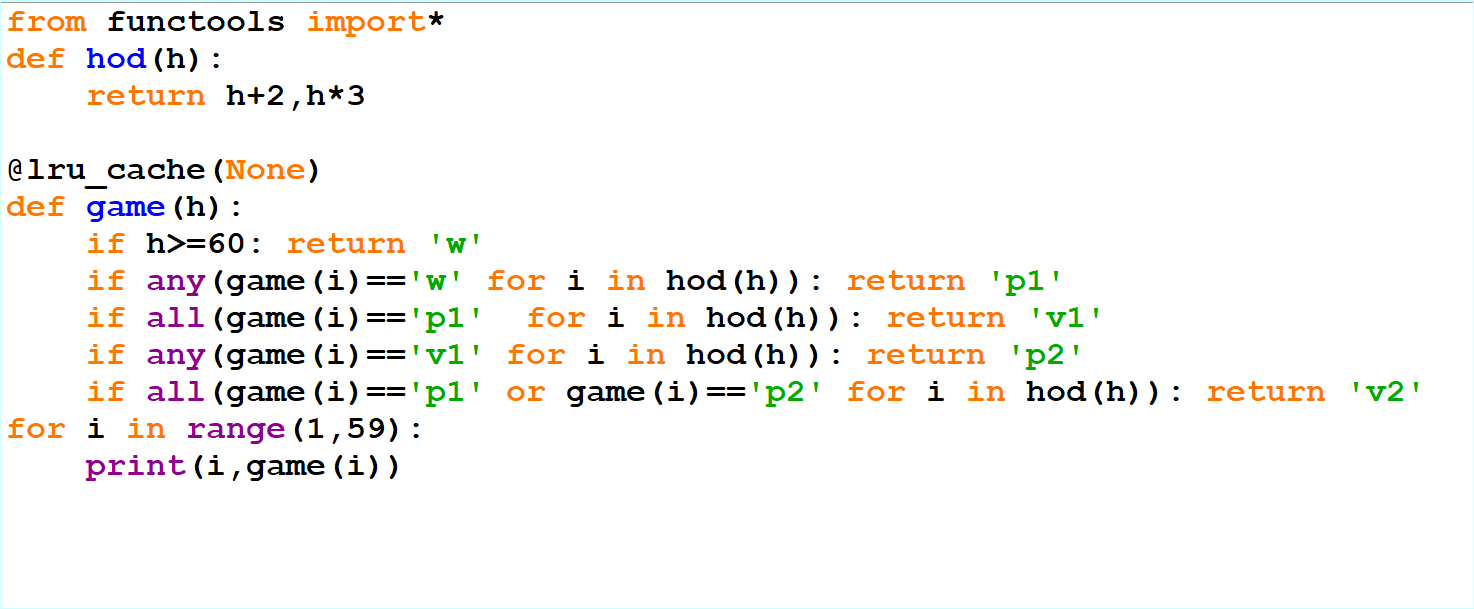
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 4: #Условия завершения игры
return p == 4
if p % 2! = 0:
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or\
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
else:
return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and\
f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)
20. 2 кучи.
def e(x1,x2,s):
if x1+x2>=77 and s==4:
return True
else:
if x1+x2<77 and s==4:
return False
else:
if x1+x2>=77:
return False
if s%2==1:
return e(x1+1,x2,s+1) or e(x1,x2+1,s+1) or e(x1*2,x2,s+1) or e(x1,x2*2,s+1)
else:
return e(x1+1,x2,s+1) and e(x1,x2+1,s+1) and e(x1*2,x2,s+1) and e(x1,x2*2,s+1)
for i in range (1,150+1):
if e(7,i, 1):
print(i)
21. 2 кучи.
def f(x, y,p):
if x+y>=142 and (p==5 or p==3):
return True
else:
if x+y<142 and p==5:
return False
else:
if x+y>=142:
return False
if p%2==0:
return f(x+2,y, p+1) or f(x*2,y, p+1) or f(x, y+2,p+1) or f(x, y*2,p+1)
else:
return f(x+2,y, p+1) and f(x*2,y, p+1) and f(x, y+2,p+1) and f(x, y*2,p+1)
def f1(x, y,p):
if x+y>=142 and p==3:
return True
else:
if x+y<142 and p==5:
return False
else:
if x+y>=142:
return False
if p%2==0:
return f1(x+2,y, p+1) or f1(x*2,y, p+1) or f1(x, y+2,p+1) or f1(x, y*2,p+1)
else:
return f1(x+2,y, p+1) and f1(x*2,y, p+1) and f1(x, y+2,p+1) and f1(x, y*2,p+1)
for i in range(1,150+1):
if f(2,i, 1):
print (i)
for i in range(1,150+1):
if f1(2,i, 1):
print (i)
Материалы ученикам

ЕГЭ. Информатика. Справочный материал — 2022.

ОГЭ. Методика подготовки к ОГЭ — 2018.

ОГЭ. Пособие — разбор второй части ОГЭ 2020

ОГЭ. Информатика. 13 задание

Возможные темы проектно-исследовательских работ по информатике