В городе M расположена кольцевая автодорога длиной в N километров с движением в обе стороны. На каждом километре автодороги расположены пункты приема мусора определенной вместимости. В пределах кольцевой дороги в одном из пунктов сборки мусора собираются поставить мусороперерабатывающий завод таким образом, чтобы стоимость доставки мусора была минимальной. Стоимость доставки мусора вычисляется, как вместимость пункта сбора умноженная на расстояние от пункта сбора мусора до мусороперерабатывающего завода. Если мусороперерабатывающий завод находится рядом с пунктом сбора расстояние считается нулевым. Контейнеры нумеруются с 1 до N.
Рядом с каким пунктом сбора мусора нужно поставить мусороперерабатывающий завод?
Дана последовательность натуральных чисел. Необходимо определить количество её непрерывных подпоследовательностей, сумма элементов которых кратна 999.
Входные данные
Первая строка входного файла содержит целое число N — общее количество чисел в наборе. Каждая из следующих N строк содержит одно число.
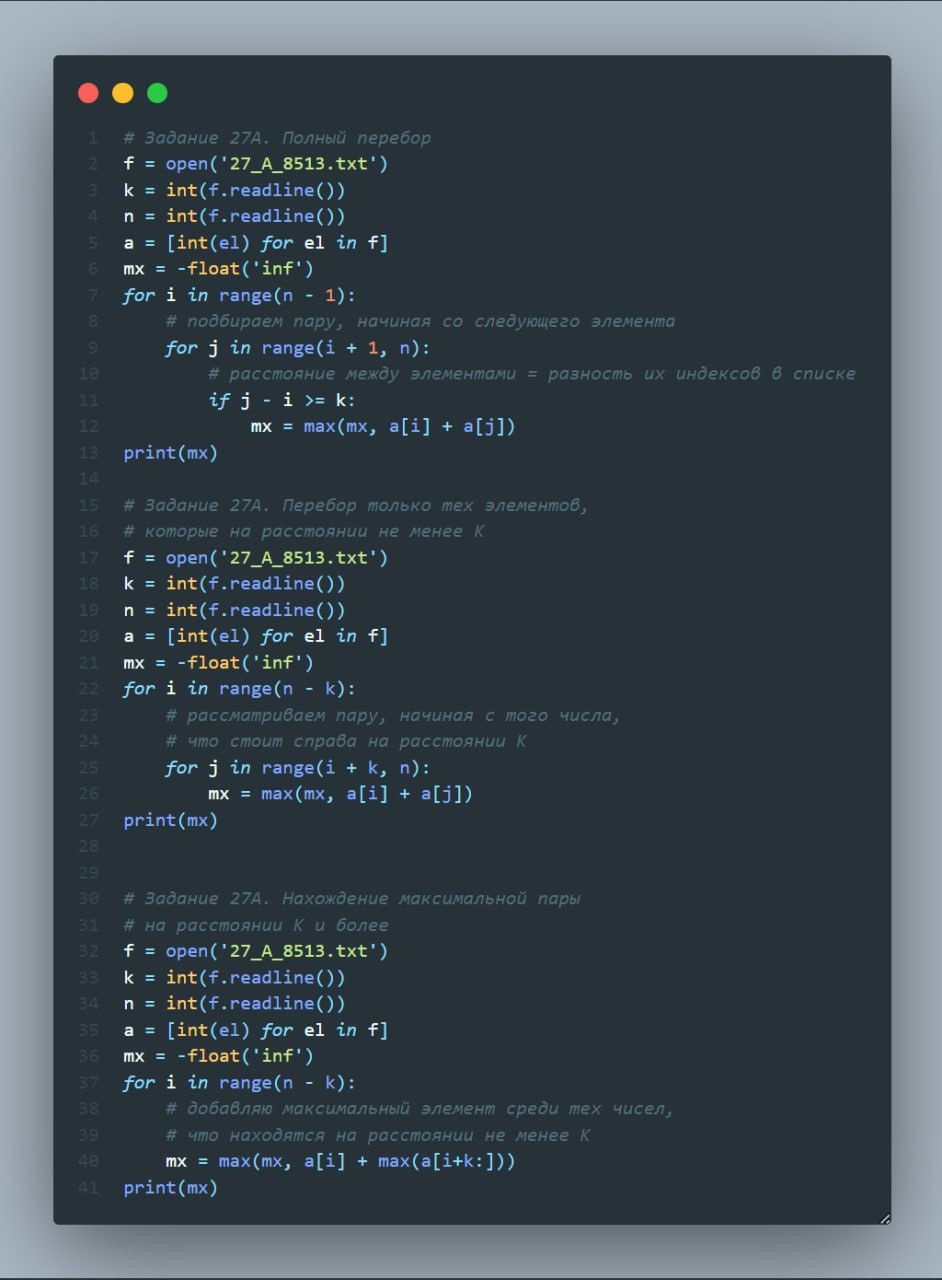
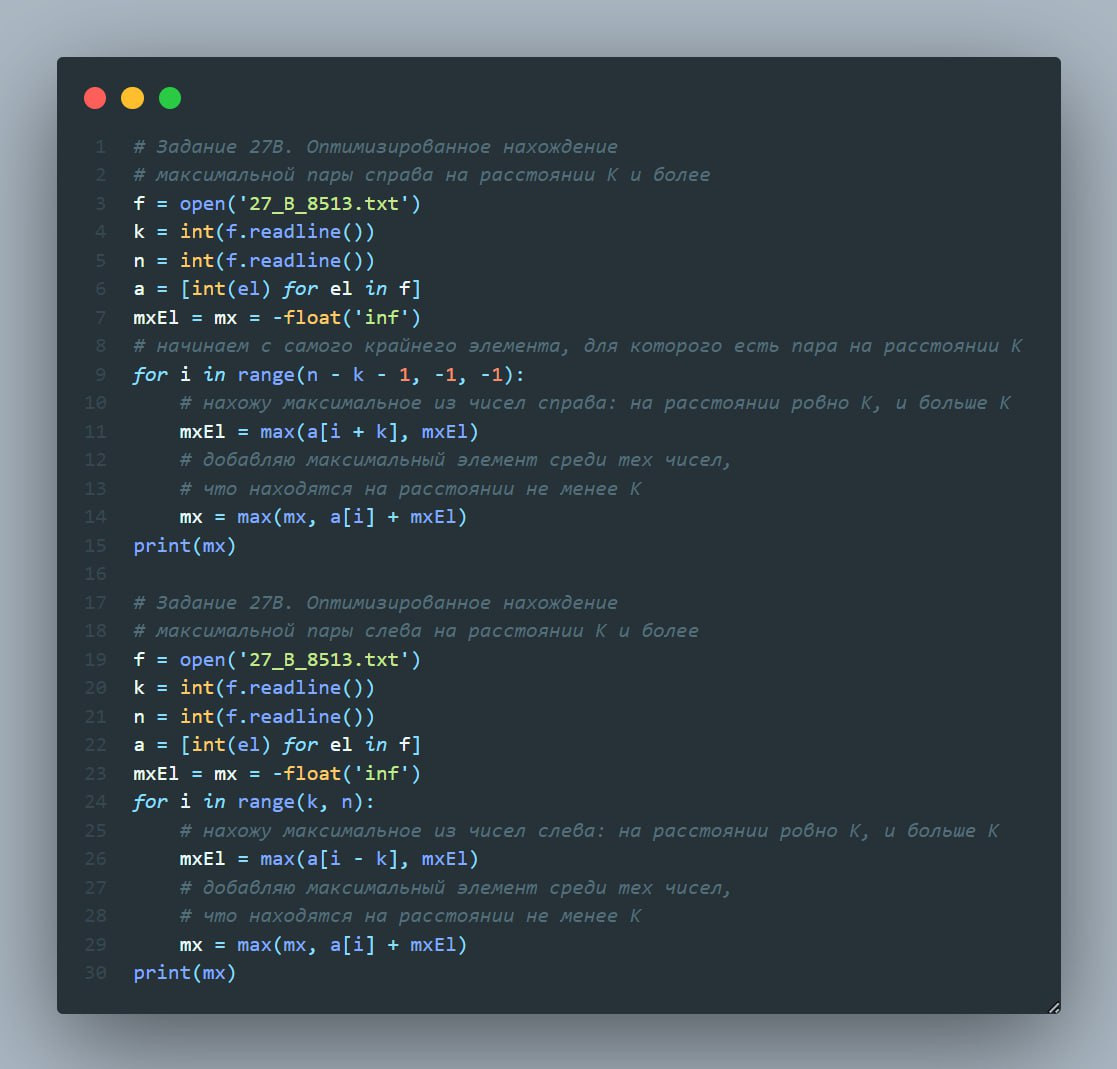
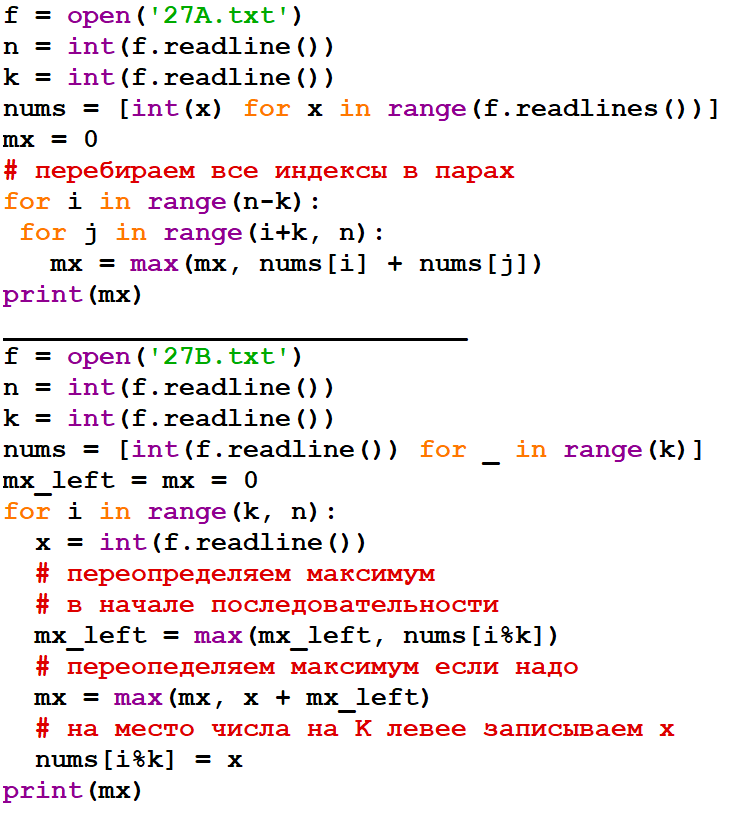
Метеорологическая станция ведёт наблюдение за количеством выпавших осадков. Показания записываются каждую минуту в течении N минут. Определяется пара измерений, между которыми прошло не менее K минут. Найдите максимальную сумму показаний среди таких пар.
Входные данные
Даны два входных файла (A и B), каждый из которых в первой строке содержит число N — количество измерений, во второй строке K — минимальное количество минут между искомыми измерениями. В каждой из следующих N строк находится число: количество выпавших осадков.
В ответе укажите два числа: сначала значение искомой величины для файла A, затем — для файла B.
По каналу связи передаётся последовательность целых неотрицательных чисел — показания прибора, полученные с интервалом в 1 мин. в течение T мин. (T — целое число). Прибор измеряет количество атмосферных осадков, полученное регистратором за минуту, предшествующую моменту регистрации, и передаёт это значение в условных единицах измерения.
Определите два таких переданных числа, чтобы между моментами их передачи прошло не менее K мин., а их сумма была максимально возможной. Укажите найденное суммарное количество осадков.
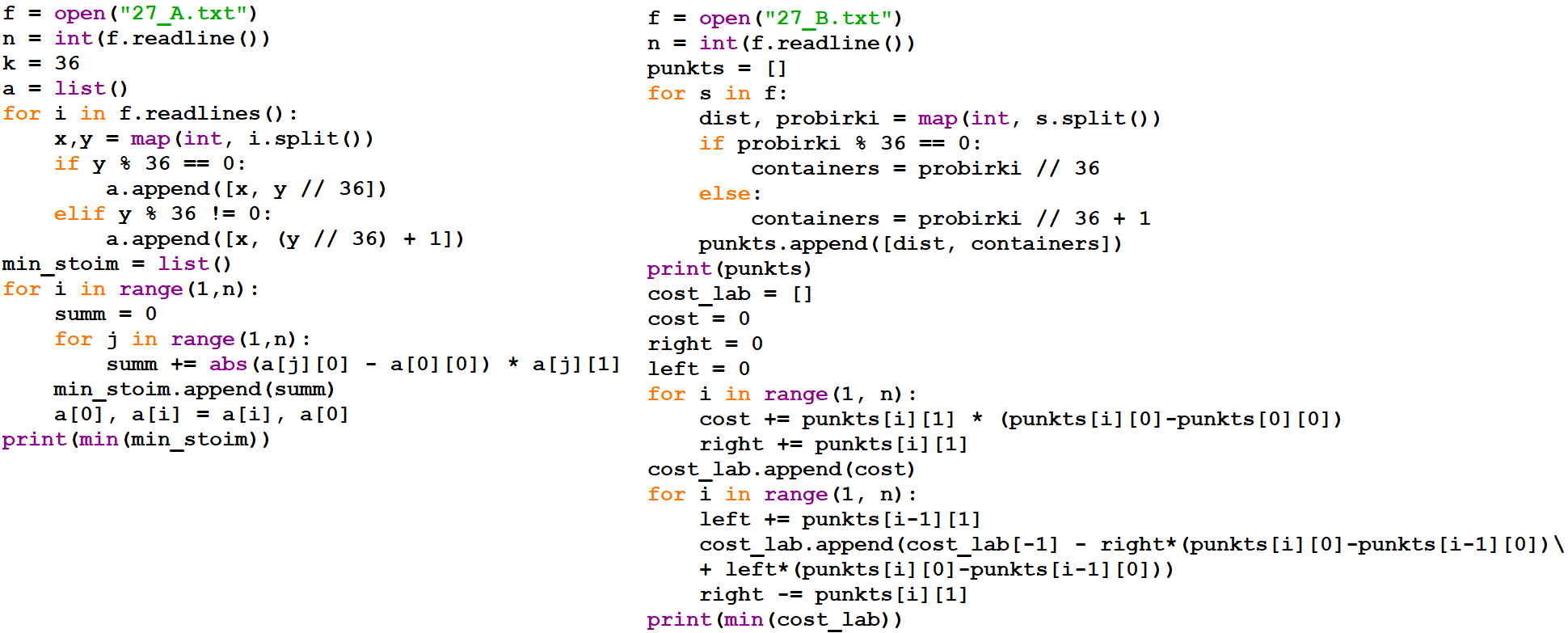
У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.
Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Вариант 1.
Важно при решении не забыть про расчет РАЗНИЦЫ между значениями в каждой строке.
Имеется набор данных, состоящий из пар положительных целых чисел. Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел не делилась на 3 и при этом была максимально возможной. Гарантируется, что искомую сумму получить можно. Программа должна напечатать одно число — максимально возможную сумму, соответствующую условиям задачи.
Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество пар N (1 ≤ N ≤ 100000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 10 000.
Вариант 2.
Компьютер наземной станции слежения получает от объектов-самолётов, находящихся в зоне её работы, идентификационные сигналы, представляющие собой последовательность из N целых положительных чисел. Каждый объект направляет на наземную станцию уникальное число, т. е. все числа в получаемой станцией последовательности различны. Обработка сигнала представляет собой рассмотрение всех пар различных элементов последовательности, при этом элементы пары не обязаны быть переданы непосредственно друг за другом, порядок элементов в паре не важен. Считается, что возникла одна критическая ситуация, если произведение элементов некоторой пары кратно 58.
Необходимо определить общее количество возникших критических ситуаций.
Пояснение:
Произведение двух чисел делится на 58, если выполнено одно из следующих условий (условия не могут выполняться одновременно).
A. Оба сомножителя делятся на 58.
Б. Один из сомножителей делится на 58, а другой не делится.
B. Ни один из сомножителей не делится на 58, но один сомножитель делится на 2, а другой — на 29.
Почему именно 2 и 29?
Берем два делителя числа 58, произведение которых дает число 58: 2*29 = 58. При этом одно из них — наименьший делитель (в нашем случае 2), а другой, не должен делиться на первый найденный делитель (29/2 <> 0).
Условие делимости произведения на 58 можно сформулировать проще, например так:
(один из сомножителей делится на 58)
ИЛИ
(один сомножитель делится на 2, а другой — на 29)
Но в этом случае пара сомножителей может удовлетворять обоим условиям, что затруднит подсчёт количества пар.
При вводе чисел можно определять, делится ли каждое из них на 58, 2 и 29, и подсчитывать следующие значения:
n58 — количество чисел, кратных 58;
n29 —количество чисел, кратных 29, но не кратных 2 и 58;
n2 — количество чисел, кратных 2, но не кратных 29 и 58.
Сами числа при этом можно не хранить. Каждое число учитывается не более чем в одном из счётчиков.
Количество пар, удовлетворяющих условию А, можно вычислить по формуле n58*(n58 — 1)/2.
Количество пар, удовлетворяющих условию Б, можно вычислить по формуле n58*(N — n58).
Количество пар, удовлетворяющих условию В, можно вычислить по формуле n2 * n29.
Поэтому искомое количество пар вычисляется по формуле:
n58 * (n58 — 1)/2 + n58 * (N — n58) + n2 * n29
n=int(input())
n58,n29,n2=0,0,0
for i in range(n):
a=int(input())
if a % 28 == 0:
n58+=1
elif a % 29 == 0:
n29+=1
elif a % 2 == 0:
n2+=1
k58=n58 * (n58-1) // 2 + n58 * (n-n58) + n2 * n29
print(k58)
Материалы ученикам

ОГЭ. Информатика. 13 задание

Возможные темы проектно-исследовательских работ по информатике

Таблица перевода систем счисления. Таблица степеней. Свойства степеней

Хорошее поведение
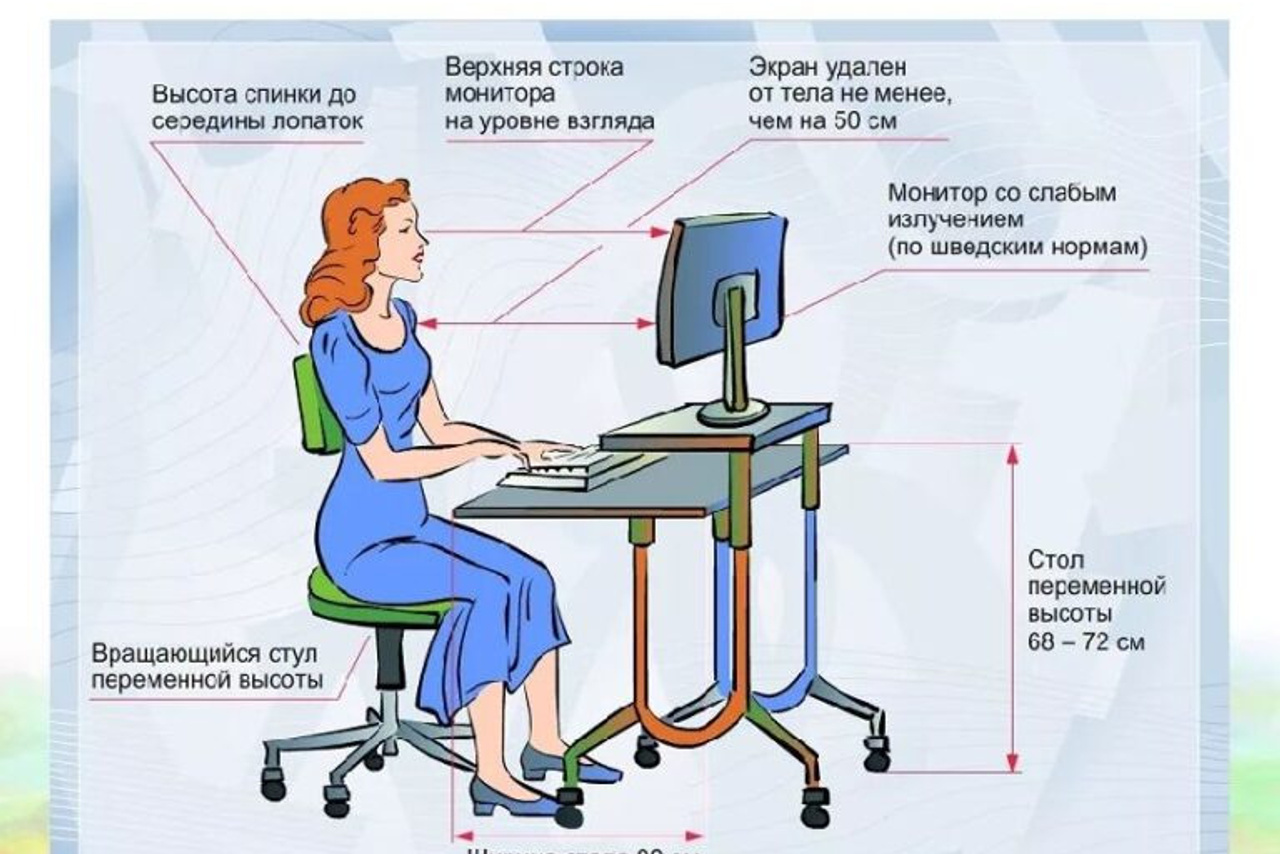
Обязательные требования при работе в компьютерном классе
Практика без теории — путь в никуда

Правильный подход к выполнению домашнего задания и мои требования

О воспитании и подготовке домашнего задания