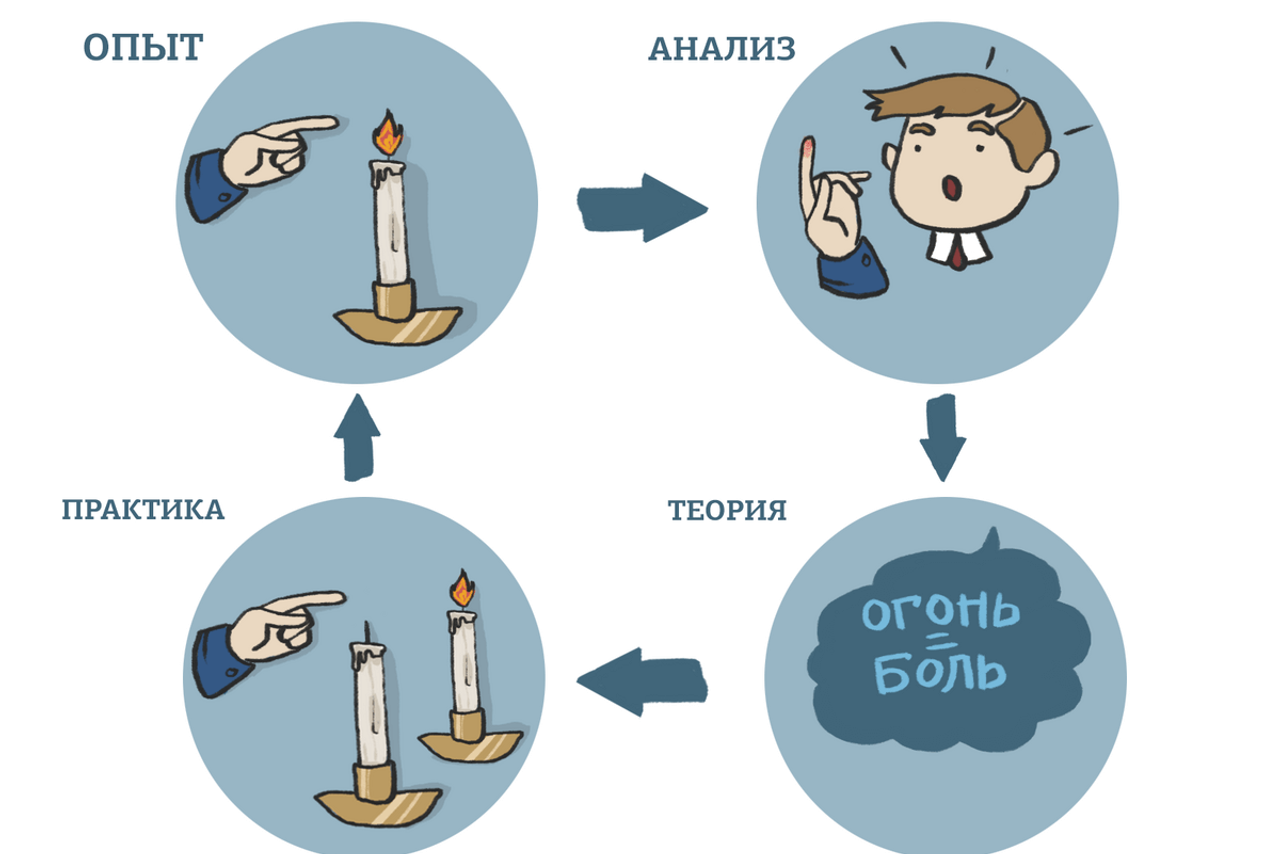
Маска числа — это последовательность цифр, в которой могут встречаться специальные символы «?» и «*». Символ «?» означает ровно одну произвольную цифру, символ «*» означает произвольную (в том числе пустую) последовательность цифр.
Пример. Маске 123*4? 5 соответствуют числа 123 405 и 12 376 415.
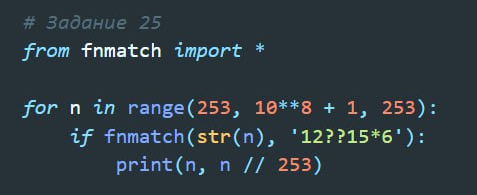
Найдите все натуральные числа, не превышающие 1010, которые соответствуют маске 1? 493*41 и при этом без остатка делятся на 2023. В ответе запишите все найденные числа в порядке возрастания.
Найдите все натуральные числа, не превышающие 10**10, которые соответствуют маске 1? 7246*1 и при этом без остатка делятся на 4173.
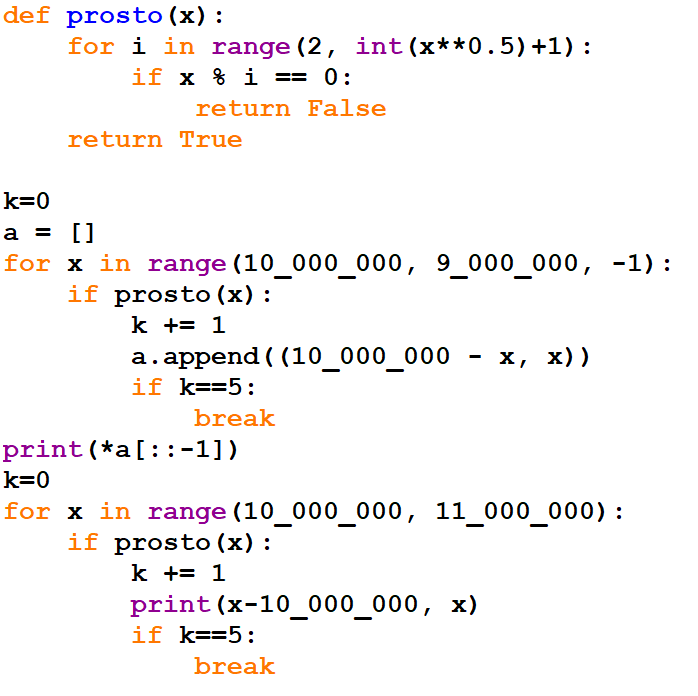
Напишите программу, которая находит 10 простых чисел наиболее приближенные к числу 10000000 (10 миллионов). Причем 5 найденных чисел должны быть меньше заданного числа, остальные 5 чисел-больше.
Найденные числа расположите в порядке возрастания. В качестве ответа выведите пары чисел — расстояние от найденного числа до 10000000 и само число.
Пусть M(k) = 9 000 000 + k, где k — натуральное число.
Найдите пять наименьших значений k, при которых M(k) нельзя представить в виде произведения трёх различных натуральных чисел, не равных 1.
В ответе запишите найденные значения k в порядке возрастания.
Вариант 1.
for i in range(101000000, 102000000 + 1, 2):
k = 1
d = 2
while d * d < i:
if i % d == 0:
if d % 2 == 0:
k += 1
if (i//d) % 2 == 0:
k += 1
if k > 3:
break
d += 1
if d * d == i:
k += 1
if k == 3:
print(i)
Вариант 2.
Ищет среди целых чисел, принадлежащих числовому отрезку [312614; 312651], числа, имеющие ровно шесть различных натуральных делителей. Для каждого найденного числа запишите эти шесть делителей в шесть соседних столбцов на экране с новой строки. Делители в строке должны следовать в порядке возрастания.
for i in range(312614,312652):
cnt=0
v=[]
for j in range(1,i+1):
if i%j==0:
cnt+=1
v.append(j)
if cnt==6:
print(v)
Вариант 3.
Пусть M(N) — пятый по величине делитель натурального числа N
без учёта самого числа и единицы. Найдите 5 наименьших натуральных чисел, превышающих 460 000 000, для которых M(N) > 0.
n=460000000
count=0
while count! =5:
n+=1
countd=0
for d in range(2,n//2+1):
if n%d==0:
coutd+=1
if
countd==5:
print(n//d)
count+=1
break
Вариант 4.
Назовём натуральное число подходящим, если у него ровно 3 различных простых делителя. Например, число 180 подходящее (его простые делители — 2, 3 и 5), а число 12 — нет (у него только два различных простых делителя). Определите количество подходящих чисел, принадлежащих отрезку [10001; 50000], а также наименьшее из таких чисел. В ответе запишите два целых числа: сначала количество, затем наименьшее число.
def PrimeDelThree(n):
SetPrimeDel = set()
prime = True
for d in range(2, n+1):
while n % d == 0:
SetPrimeDel.add(d)
prime = False
n = n // d
if n == 1:
break
else:
if (d*d>n) and prime:
break
if prime:
SetPrimeDel.add(n)
return len(SetPrimeDel)==3
(count, mn) = (0, 50_000)
for n in range (50_000, 10001-1, -1):
if PrimeDelThree(n):
count += 1
mn = n
print(count, mn)
Вариант 5.
Найдите все натуральные числа, принадлежащие отрезку [35000000; 40000000], у которых ровно пять различных нечётных делителей (количество чётных делителей может быть любым). В ответе перечислите найденные числа в порядке возрастания.
Идея. Нас интересуют числа, являющиеся четвертой степенью простого числа, возможно умноженные на некоторую степень двойки.
def isPrime(n):
d = 2
while d * d <= n:
if n % d == 0:
return False
d += 1
return True
(a, b) = (35_000_000, 40_000_000)
for n in range (a, b+1):
x = n
while x % 2 == 0:
x = x // 2 # Убираем все четные делители
if x ** 0.25 == int(x ** 0.25) and isPrime(x ** 0.25):
print(n)
n += 1
Пусть M (N) — произведение 5 наименьших различных натуральных делителей натурального числа N, не считая единицы. Если у числа N меньше 5 таких делителей, то M (N) считается равным нулю.
Найдите 5 наименьших натуральных чисел, превышающих 200 000 000, для которых 0 < M (N) < N.
В ответе запишите найденные значения M (N) в порядке возрастания соответствующих им чисел N.
Материалы ученикам

ЕГЭ. Информатика. Справочный материал — 2022.

ОГЭ. Методика подготовки к ОГЭ — 2018.

ОГЭ. Пособие — разбор второй части ОГЭ 2020

ОГЭ. Информатика. 13 задание

Возможные темы проектно-исследовательских работ по информатике

Таблица перевода систем счисления. Таблица степеней. Свойства степеней

Хорошее поведение
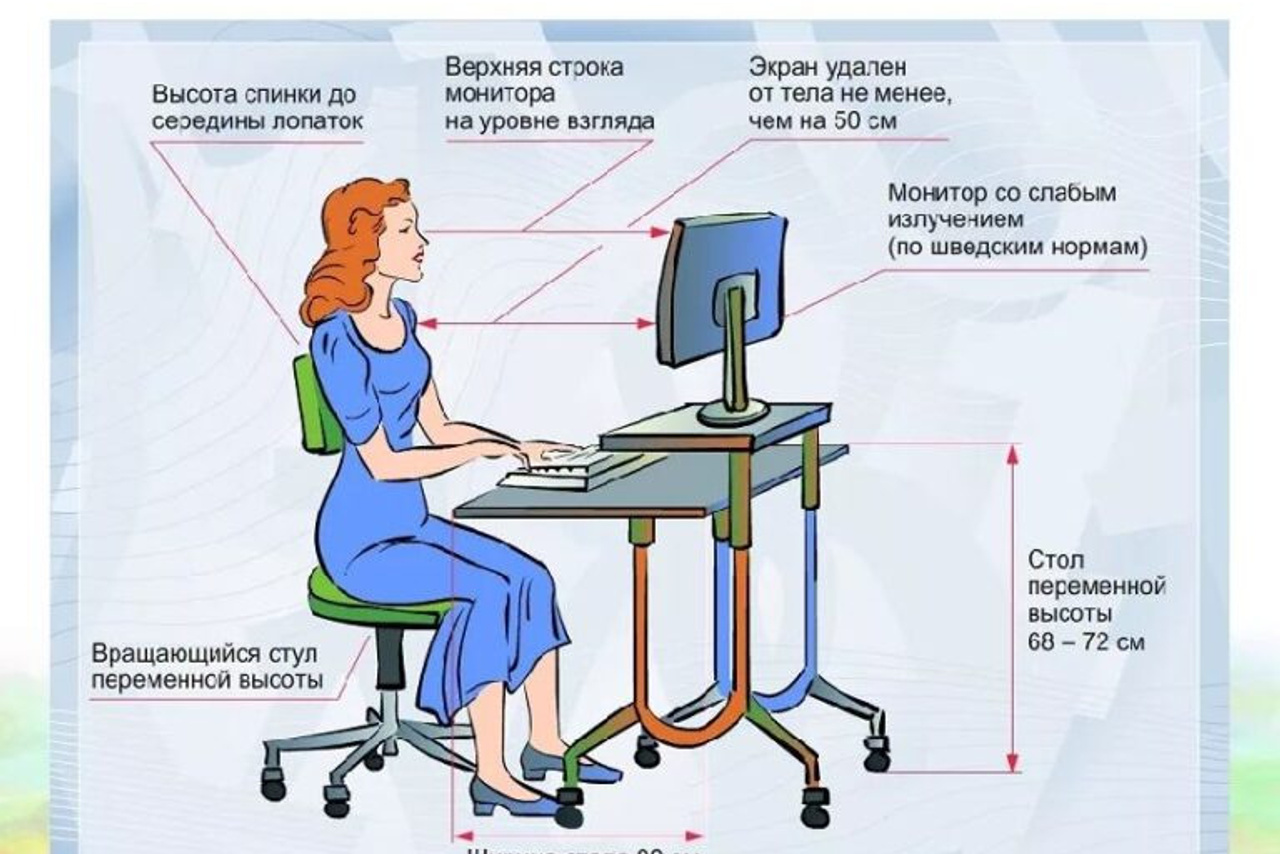
Обязательные требования при работе в компьютерном классе