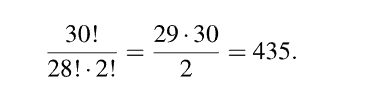ЕГЭ. Информатика. 16 задание.

def F(n):

    if n > 2:

        return F(n-1)+ G(n-2)

    else: return 1

def G(n):

    if n > 2:

        return G(n-1) + F(n-2)

    else: return 1

print(F(8))

def F(n):

    if n > 2:

        return F(n-1)+G(n-1)+F(n-2)

    else: return n

def G(n):

    if n > 2:

        return G(n-1)+F(n-1)+G(n-2)

    else: return 3-n

print(G(5))

f=[0]*1000000000

count=0

for i in range(1,len(f)):

    if i%2==1:

        f[i]=f[i-1]+1

        if f[i]==2:

            count+=1

    else:

        f[i]=f[i//2]

        if f[i]==2:

            count+=1

print(count)

def g(n):

    if n//10%10==9:

        return n

    else:

        return n+10

def f(x, y):

    if x==y:

        return 1

    if x>y or x==25:

        return 0

    if x<y:

        return f(x+1,y) +f(x*2,y) +f(x*3,y)

print(f(3,12)*f(12,46))

Алгоритм вычисления значения функции F(n), где n  — целое неотрицательное число, задан следующими соотношениями:

F(0) = 0;

F(n) = F(n − 1) + n.

Укажите количество таких чисел n из интервала 765 432 010 ≤ n ≤ 1 542 613 234, для которых F(n) не делится без остатка на 3.

Заметим, что функция не делится на 3, когда ее значение от деления на 3 даст остаток 1, составим программу на языке Python.

print((1542613234 — 765432010) //3 +1)

Алгоритм вычисления значения функции F(n), где n  — целое неотрицательное число, задан следующими соотношениями:

F(0) = 0;

F(n) = F(n − 1) + 1, если n нечётно;

F(n) = F(n / 2), если n > 0 и при этом n чётно.

Укажите количество таких значений n < 1 000 000 000, для которых F(n)  =  3.

k = 0

for i in range(2, 31):

    k = k + i — 1

print(k)